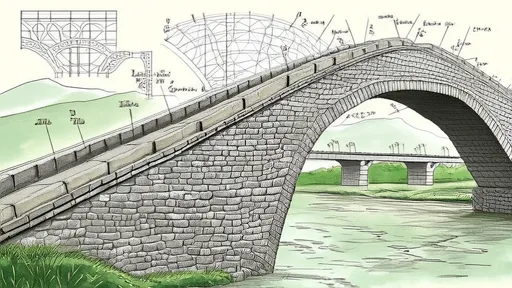
In the realm of civil engineering, few structures capture the imagination quite like the stone arch bridge. These timeless marvels, which have gracefully spanned rivers and valleys for millennia, represent a perfect fusion of artistry and scientific precision. While their aesthetic appeal is undeniable, the true genius of these structures lies hidden within their carefully calculated stress distributions—a topic that has fascinated engineers and mathematicians for centuries. Recent advancements in computational modeling have breathed new life into this ancient engineering form, allowing researchers to develop increasingly sophisticated mathematical frameworks to understand and predict how these structures bear their loads.

The fundamental challenge in analyzing stone arch bridges lies in their unique load-bearing mechanism. Unlike modern steel or concrete bridges that rely on the tensile strength of their materials, traditional stone arches operate entirely in compression. Each stone voussoir presses against its neighbors, transferring weight laterally along the curve of the arch until it reaches the abutments. This elegant system creates a complex three-dimensional stress field that varies throughout the structure. The development of accurate mathematical models requires accounting for numerous variables including the arch's geometry, the properties of the masonry materials, and the patterns of loading the bridge will experience throughout its lifetime.

Modern research approaches this challenge through several complementary mathematical frameworks. Continuum mechanics models treat the masonry as a homogeneous material with equivalent properties, while discrete element methods simulate the individual stones and their interactions. Meanwhile, limit analysis techniques help engineers understand the collapse mechanisms that occur when loads exceed the structure's capacity. Each approach offers distinct advantages and limitations, leading researchers to increasingly combine multiple methodologies to create more comprehensive models that can predict stress distributions with remarkable accuracy.

The geometry of the arch itself represents perhaps the most critical factor in stress distribution. The Roman semicircular arch, the Gothic pointed arch, and the Renaissance segmental arch each create dramatically different stress patterns. Modern researchers have developed sophisticated parametric models that can adjust the arch's shape, thickness, and rise-to-span ratio to optimize stress distribution. These models reveal how subtle changes in geometry can significantly alter how forces flow through the structure, sometimes reducing peak stresses by impressive margins while maintaining the bridge's structural integrity and aesthetic character.

Material properties present another layer of complexity in modeling stone arch behavior. Natural stone possesses anisotropic qualities—its strength varies depending on the direction of loading relative to its bedding planes. Furthermore, the mortar joints between stones introduce compliance that affects how stresses redistribute throughout the structure. Advanced models now incorporate these material complexities through sophisticated constitutive equations that account for nonlinear behavior, cracking, and even the gradual deterioration of materials over time. This allows engineers to predict not just how a new bridge will perform, but how an ancient structure might behave after centuries of service.

Loading conditions add further dimensions to the modeling challenge. Stone arches must withstand not only their own weight but also live loads from traffic, environmental forces from wind and water, and even seismic activity in earthquake-prone regions. Researchers have developed dynamic models that can simulate how stresses propagate through the structure when subjected to moving loads or ground vibrations. These models reveal fascinating phenomena such as how certain load positions create hinge points that temporarily change the structural system, and how the mass of the structure itself provides damping that helps dissipate dynamic forces.

The validation of these mathematical models presents its own set of challenges and opportunities. Researchers employ various techniques to verify their predictions, from laboratory testing of scale models to sophisticated field measurements on existing bridges. Fiber optic sensors, laser scanning, and digital image correlation techniques now allow engineers to measure strain distributions in actual stone arches with unprecedented precision. These measurements frequently reveal unexpected stress patterns that lead to refinements in the mathematical models, creating a virtuous cycle of improvement that enhances both our theoretical understanding and practical design capabilities.

Perhaps the most exciting development in this field lies in the application of machine learning techniques to predict stress distributions. By training neural networks on vast datasets generated from both physical measurements and existing mathematical models, researchers are developing systems that can almost instantly predict stress patterns for novel arch designs. These AI-assisted approaches don't replace traditional mathematical modeling but rather complement it, helping engineers quickly evaluate numerous design alternatives before applying more rigorous analytical methods to the most promising options.

The implications of improved stress modeling extend far beyond academic interest. As preservation engineers work to maintain historic stone bridges, accurate stress analysis helps them identify vulnerable areas before failures occur. For new construction, advanced modeling enables designers to create more efficient structures that use material more economically while maintaining safety margins. Some researchers are even exploring how these principles might be applied to novel materials and construction techniques, potentially leading to a new generation of stone-inspired structures that marry ancient wisdom with cutting-edge technology.

Looking forward, the field continues to evolve at an accelerating pace. Researchers are beginning to incorporate temporal factors into their models, simulating how stress distributions change as materials creep and relax over decades or even centuries. Others are working to develop unified modeling approaches that can seamlessly transition between micro-scale analysis of individual stone interactions and macro-scale assessment of overall structural behavior. These advances promise to deepen our understanding of these magnificent structures while ensuring that the art and science of stone arch bridge construction continues to evolve and inspire future generations of engineers and architects.

What becomes clear through this ongoing research is that the stone arch bridge, often perceived as a relic of historical engineering, remains remarkably relevant in the modern world. The mathematical models being developed today not only help us preserve our architectural heritage but also contribute to sustainable construction practices for the future. As we continue to refine our understanding of stress distribution in these elegant structures, we reaffirm the enduring truth that good engineering, like the stone arches themselves, stands the test of time through careful calculation, respect for materials, and harmonious balance between form and function.